The example problem which follows goes through a comprehensive local stress analysis of a vessel/nozzle using WRC 107 criteria.
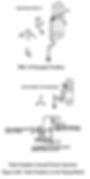
In the figure, the user may also notice that there are two nodes occupying the same space at the nozzle/vessel surface junction: nodes 55 and 56. An anchor at 55 with a connecting node at 56 could be used to model the local vessel flexibility as "rigid". The anchor could then be replaced with a WRC 297 local vessel flexibility model, and the job be rerun to get a good idea of the "range" of loads and displacements that exist in the system around the vessel nozzle. In either case, the various restraint loads (forces and moments due to sustained, expansion and occasional loads) can be obtained from the appropriate CAESAR II restraint report. These loads reflect the action of the piping on the vessel. The sustained and expansion restraint report of the "rigid" anchor model are shown in Figure 3-70. For purposes of illustration, both the global system loads and the corresponding local WRC 107 loads are summarized in Figure 3-71.
The total sustained axial load on the nozzle may not be reflected in the restraint report. A pressure thrust load will contribute an additional axial load to the nozzle. The pressure thrust force always tends to push the nozzle away from the vessel. For example, with a pressure of 275 psi over the inside area of the 12 inch pipe, the total P load becomes:
P = -26 - P(A) = -26 - 275 p (12^2) / 4 = -31,128
The P load may be adjusted automatically for the input by CAESAR II's WRC 107 module, if the user so requests.
The actual preparation of the WRC 107 calculation input can now begin. One of the most important steps in the WRC 107 procedure is to identify the correlation between the CAESAR II global coordinates and the WRC 107 local axes. The CAESAR II program performs this conversion automatically. The user will, however, have to identify the vectors defining the vessel as well as the nozzle centerline. The following figure is provided to illustrate the definition of the direction vectors of the vessel and the nozzle.
Notice that in order to define a vessel direction vector, the user first needs to designate the output data points (A->D) as defined by the WRC 107 Bulletin. Note that the line between data points B and A defines the vessel centerline (except for nozzles on heads, where the vessel centerline will have to be defined along a direction which is perpendicular to that of the nozzle). Since, in the vessel/nozzle configuration shown, point A is assigned to the bottom of the nozzle, the vessel direction vector can be written as (0.0, -1.0, 0.0), while the nozzle direction vector is (1.0, 0.0, 0.0). The nozzle direction vector is always defined as the vector pointing from the vessel nozzle connection to the centerline of vessel.
The program first prompts the user for the entries of geometric data describing both the vessel and nozzle, followed by spreadsheets for loadings. The values of the geometric entries in this example are shown in the following printouts from the program.
The user may enter up to three sets of loadings representing Sustained (SUS), Expansion (EXP), and Occasional (OCC) load cases. The program automatically performs the stress calculation of each of the load cases consecutively. In the present case, we only have to be concerned about the sustained and thermal expansion cases. The loads are shown in the following two screens. The user can elect to leave any input cells blank if they are found not applicable. After checking all the entries made, the user should press [Fl] to initiate the analysis.
After the input echo, the parameters extracted from the WRC 107 figures are printed on the screen. This step is similar to determining the data by hand. These non-dimensional values are combined with the nozzle loads to calculate the two normal stresses and one shear stress. The stresses will be reported on the outer and inner vessel surfaces (upper & lower, respectively) of the four points A, B, C & D located around the nozzle. The program provides the normal and shear stresses and translates them into stress intensities which can be used for comparisons against material allowables.
The output of the stress computations are shown in the four pages shown in Figure 3-75. As the output shows, the largest expansion stress intensity (117475 psi) occurs at the outer surface of point B (Bu).
Read More:
Located in Calgary Alberta, We offer our Piping Engineering Services across Calgary Alberta Canada. To get our Piping Stress Analysis Services, please contact our Engineering company.
Our professional piping stress engineers have a bachelor's degree in mechanical / structural engineering and province licence (P.Eng.) in Alberta, Saskatchewan, British Columbia and Ontario. We review, validate, certify and stamp piping and structural packages.