2.3.5 Simplified Expansion Stress Check
- Meena Rezkallah, P.Eng.

- Jun 3, 2020
- 2 min read
Updated: Dec 19, 2020
The concept that addition of expansion loops reduces the expansion stress range in a system is recognized by the B31.3 code (and others). This is codified in the requirement that expansion analysis need not be explicitly done for a system meeting the following conditions:
the system is all of the same size, material, etc.,
the system has no branches, and consists of only a single run between two anchors,
there are no intermediate restraint points (note that hangers are traditionally excluded from consideration as restraints), and
Dy/(L-U)^2 < 0.03
Where: D = pipe outer diameter, inches y = resultant thermal growth to be absorbed, inches L = total length of piping, feet U = straight line distance between anchors, feet
The term (L - U) represents the amount of extra pipe (i.e., loops) in the system. Examination of this equation reveals that, after factoring through constants, it is simply a form of the guided cantilever stress equation:
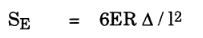
This simplified check can be illustrated by applying it to the system shown in Figure 2-12. It is clear that this system meets the first three criteria — the system is all of the same size, material, etc.; the system has no branches, and consists of only a single run between two anchors; and there are no intermediate restraint points except hangers. For the fourth requirement:

Therefore the system illustrated in Figure 2-12 need not be explicitly analyzed for expansion stresses.
How accurate is this simplified expansion stress check? Based upon the ratio of 0.0089 to 0.03 = .2968, one can infer that this system is stressed to approximately 29.68% of its allowable stress. Assuming a low carbon steel of type A106 Grade B or similar and fewer than 7,000 expected cycles, the allowable stress of the system at 350°F can be conservatively estimated as:
f (1.25 SC + 0.25 Sh) = 1.0(1.25 x 20,000 + 0.25 x 20,000) = 30,000 psi
This would imply that the maximum expansion stress in the system is somewhere in the range of:
SEmax = 0.2968 x 30,000 = 8903 psi
Figure 2-24 shows the actual maximum expansion stress found in this system through an actual CAESAR II stress analysis—9051 psi (within 1%), which demonstrates the accuracy (at least for this particular case) of this simplified method.

Read More:
To get our piping stress analysis services, please contact our piping engineering firm for a free quote.
